Constraint Optimization with Support Vector Machine

Welcome to the 24th part of our machine learning tutorial series and the next part in our Support Vector Machine section. In this tutorial, we're going to further discuss constraint optimization in terms of our SVM.

In the previous tutorial, we left off with the formal Support Vector Machine constraint optimization problem:

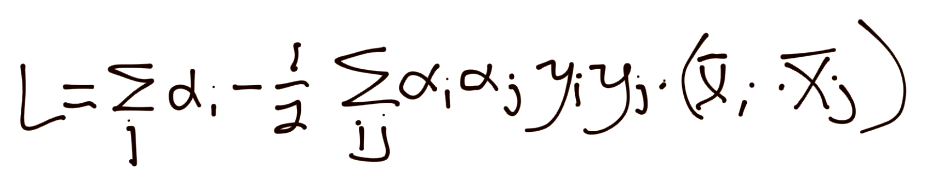
That's looking pretty ugly, and, due to the alpha squared, we're looking at a quadratic programming problem, which is not a walk in the park. Isn't constraint optimization a massive field though? Is there any other way? Well I am glad you asked, because yes, there are other ways. The SVM's optimization problem is a convex problem, where the convex shape is the magnitude of vector w:

The objective of this convex problem is to find the minimum magnitude of vector w. One way to solve convex problems is by "stepping down" until you cannot get any further down. You will start with a large step, quickly getting down. Once you find the bottom, you are going to slowly go back the other way, repeating this until you find the absolute bottom. Think of the convex problem like a bowl, and the solution process is you dropping a ball down the inside edge of the bowl. The ball will quickly roll down the sides, go right over the perfect middle, maybe go up the other side a bit, but come back down, go the other way, and maybe repeat a bit, each time moving a bit slower overall and covering less distance until finally the ball finds rest at the bottom of the bowl.

We're going to mimic this exact same process in Python. We'll simply plug in vectors for w, starting with large magnitudes. Recall the magnitude is the square root of the sum of the squared constituents. That said, vector w could be [5,5] or [-5,5] and have the same magnitude, but of course produce a very different dot product with featuresets and a very different resulting hyperplane. For this reason, we need to check every variation of each vector.

Our basic idea is to be like the ball, quickly moving down the sides, and continuing until we notice we're no longer going down. At that point, we need to only retrace our last few steps. We'll do that with a smaller step. Then maybe repeat this process a couple more times. For example:

First, we'll begin at the top like the green line, and we'll take big steps on the way down. We'll pass the center, then take some smaller steps like the red line. Then we'll do the light blue line. This way, we wind up taking less steps overall (where in each step we compute a new version of vector w and b). This way, we can get an optimized vector w to a precise degree, without originally taking such small steps to achieve the same result and costing us much more in processing.

When and if we found that perfect bottom of the bowl/convex shape, we'd say we found the global minimum. The reason why a convex problem is nice is the very reason why we can use this step method to find the bottom. Imagine if, rather than a perfect convex shape, we had something like:

Now, while taking steps starting from the left, you might detect you are going back up, so you go back and settle in to what is known as a local minimum:

Again though, we're working with a nice convex problem, so we don't have to exactly worry about that. My plan is to give us a vector, and slowly step down the magnitude of the vector (which just means lowering the absolute value of the data inside our vector). For each vector, let's say [10,10], we'll transform that vector by the following: [1,1],[-1,1],[-1,-1], and [1,-1]. This will give us all of the variances of that vector that we need to check for, despite them all having the same magnitude. This is what we'll be working on in the next tutorial.

The next tutorial: Beginning SVM from Scratch in Python