Complex Math - Unconventional Neural Networks in Python and Tensorflow p.12

Hello and welcome to part 12 of the unconventional neural networks series, here we're just going to go over the results from the two more complex math models. First, we have the multiple-operators model, that simply tested the same thing as the additional model, where we got 100% accuracy, only this time using any of 4 operators (+,-,*,/). The model was asked to solve equations like:

83188*70507
4988+18198
21562/25607
24494/2506
2305-7721
45157*60121
50226+31208

The results here:

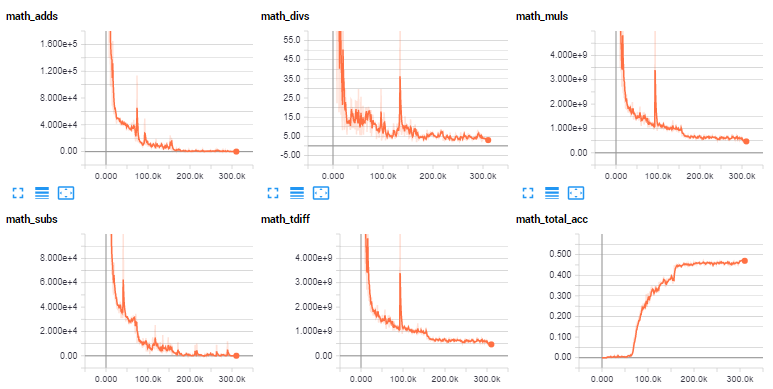
Instead of us going through the individual output files, here they are graphed directly into tensorboard (thanks Daniel!)

To get the project code used for doing this, head to this branch of the chatbot, or just pull with git clone --branch complex_math --recursive https://github.com/daniel-kukiela/nmt-chatbot.git

As you can see, the model was able to get about 45% accuracy. I imagine we could find a model to achieve 99%+ accuracy. I fairly arbitrarily built this model. There are many things we could tweak, such as layer size, number of layers, bidirectional or not, attention mechanism, and much more.

Anyway, instead I was much more curious about the far-more complex math model, which worked on equations like:

63166/21707+25193-26327+14443*20117*67066/91296
22564/(15291+65142*83720*6457+91001/70325+9577)
77861+((43454-88314*(78299/77643)+40734)/61134/46151)
90584+26054+54674
91680/(49369+(99777-91774-(1089-58896/99825*83470)/42034))
23831*58422+51593+55339
51065+96120*50507
82385*54087/45899
52283-(37808*86291+25851)*62242
58635*72485
80418/87375*(71408-38976)
52734*35731*80873-5370+89899/64551

The results here:

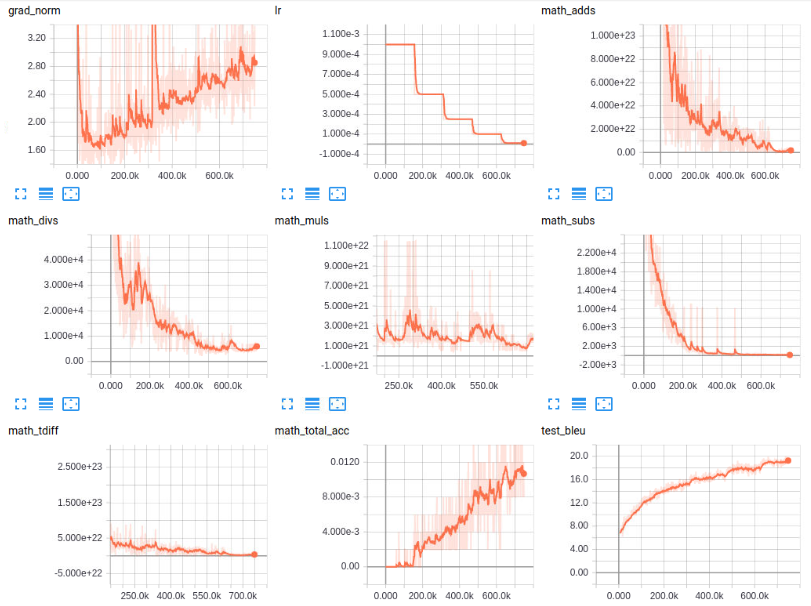
So we definitely learned a decent amount. In the end, we almost over a smoothed 1.2% accuracy. The model is still learning here, so maybe there's more to come, but I doubt we'll see it get beyond anything much past here, surely not more than 5%. That said, again, the neural network can clearly learn this type of problem, it's just that our model probably isn't ideal. Even though we only get 1% accuracy, I am still super excited about this result. The model got pretty much every prediction. It would at least pass most multiple-choice exams with equations like this!

This model is currently in 11 days of training on a P6000 GPU. As such, I have decided to host the model. You can get it here: Complex Math model. That file includes the settings that were used to create it.

The fact that it could learn complex relationships like with parenthesis and even embedded parenthesis is very impressive to me. I partially expected this model to mostly just learn noise, but no, it actually was learning.

Moving forward here, I plan to tinker around with varying models to see if I can find something that learns better. That said, I don't expect to hold your attention throuh this process. As such, I will be shifting gears a bit into playing around neural networks and audio! Using neural networks for images and language is maybe too conventional for this series! Can we teach a neural network to do speech? How about to make music? Let's see!